Waves on the Electoral Tide – a punters guide

This is a fairly long post, I’m afraid, but you can skip down to the "Fluctuation Size" section if you're confident about the Curtice findings on UNS (which were recently highlighted on the main site) and the use of standard deviations.

The point of this article is to inform the punter when looking at individual constituency odds compared to UNS. What would fair odds be if the fluctuations were random? They're not totally random, but it gives you a starting point (like "evens" for a seat that would fall exactly on UNS) from which to work.

Background – skip this if you’re familiar with the issues around using UNS

One of the biggest warnings about using Uniform National Swing (UNS) for predictions is that the swing is never uniform nationally. In the past, it was often assumed that the deviations from UNS would cancel out. In the round.

Yes, Constituency A which should have fallen on UNS didn’t (Dover, for example), but it’s okay – Constituency B, which shouldn’t have fallen (Putney, for example), did. And for every Dover, there would be a Putney. More or less.

John Curtice blew that idea out of the water at the last General Election, as highlighted by Mike recently on the main blog. The key point is that the assumption only holds if the variations in swing needed are spread pretty uniformly. So for every constituency overshoot of 3%, there would be as many seats in danger as would be saved by a constituency undershoot of 3%. And that’s not true. If more are "in reach of the waves" above the line of UNS than below, then the fluctuations should cause more extra seats should fall (those above the line) than those below the line to fail to fall, giving a net bonus to the swing - as occurred in 2005. Conversely, if the distribution has more "in reach of the waves" below the line than above, there would be a net underperformance.

Another key assumption is that the variations are essentially random – that an overshoot in a seat 2% further than the UNS would reach is as likely as an equal overshoot in a safe seat or hopeless seat. Likewise with undershoots. If a party were to concentrate its overshoots in marginals and undershoots in safe seats and hopeless cases, they would have a happy Leader on the Friday morning after the election. That's targeting, basically. Each party attempts to skew the overshoots in its own favour – Labour with more success than the Tories in the 92, 97 and 01 elections; in the 05 elections, the Tories had a little more success in targetting than Labour and noticeably more than the Lib Dems. Thiscan have an effect of shifting the entire electoral tide (“sea level”) by up to about 1% over the average swing (with poorer performances in non-battle seats).

There will be a random element, of course, but demographics, comparative local party strengths, local MP incumbency (especially good MP? Tainted by expenses?) and other local and regional factors will be prominent in increasing or decreasing the chance of the seat being held or falling. This is where you make your judgement call to adjust the odds produced assuming randomness.

There’s one more rather minor assumption – that the UNS (which is the overall swing from one party to another over the entire country) will be equal to the average swing of all constituencies. Which appears to be trivial on the face of it, but actually isn’t – and isn’t quite true. Because constituencies vary in size, it would only be true if the big constituencies behave exactly the same as the small ones – if the Isle of Wight swings 5% to the Tories from Labour, but the Western Isles swing 5% towards Labour, the average swing between constituencies is zero. But when you look at the average swing of the populations added together (the UNS), it would say 3.33% Lab to Con. On the whole, Labour tend to do a touch better than UNS due to this fact in any case (around 0.3%-0.4%), but unusually in 2005, the average constituency swing was about a quarter of a percentage point better for the Tories than the UNS - possibly because the benefit for Labour had got about as high as it could and was unwinding a touch. Note that this is different from success in targeting marginals and should be added (or subtracted) to the level of the electoral tide.

INCORRECT ASSUMPTION 1: Uniform spread of marginality so fluctuations cancel out. This is where the need to measure the fluctuations comes in – the tables at the end of this article.
INCORRECT ASSUMPTION 2: Fluctuations are random around the average. This is where your judgement comes in - it's an opportunity for the punter
INCORRECT ASSUMPTION 3: Average = UNS.

All of this is now well accepted, but it’s all qualitative to this point. A punter needs something quantitative to help inform the betting strategy. Most specifically – how big are the likely fluctuations? What kind of overshoots and undershoots are probable? In short, how high are the waves on the electoral tide?

There have been comments on the main site that “such-and-such seat would never fall due to local factors”. The local factors are all very well, but there is an electoral tide and this article should show how much effort is needed to beat it. In addition, it should indicate just how far from UNS you can realistically look for betting opportunities.

Standard deviation

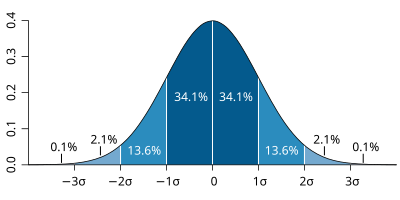
I’ve had a look at the size of the swings and fluctuations in the last five elections to get an idea. In order to show the size of the statistical noise – the variability – of a distribution of numbers (like the distribution of swings across all constituencies), mathematicians tend to use “standard deviation”. It’s also important to know what shape the distribution is. This is helped by a rule of thumb that the larger the distribution, the more it tends to the famous Bell Curve of the “normal distribution”. Looking at these elections, the swings seem to come out rather bell-curve-y all right, which means that we can say what the standard deviation means here:

(Image from Wikipedia)

68.27% of results are within 1 standard deviation above or below the mean.
90% of results are within 1.645 standard deviations of the average
95% of results are within 1.96 standard deviations of the average (as it happens, this is exactly what “Margin of Error” on opinion polls represents)
99% of results are within 2.576 standard deviations of the average
99.73% of results are within 3 standard deviations of the average.

There will be 633 632 mainland constituencies fought between Con/Lab/LD [editted] at the next election. Accordingly, for any given swing considered (say, Lab to Con), we’d expect (approximately):

430-435 seats with performance within 1 standard deviation of the swing,
135-140 between 1 and 1.645 standard deviations,
30-35 between 1.645 and 1.96 standard deviations,
24-26 between 1.96 and 2.576 standard deviations,
4-5 between 2.576 and 3 standard deviations,
1 or 2 “freak” results further than 3 standard deviations from the average constituency swing.

That’s in either direction, of course. But the crucial question is – how big is one standard deviation?

Fluctuation size:
For Lab-Con swings: standard deviation should be about 3%. The average standard deviation has been 2.89% (maximum of 3.44% in 1997, minimum of 2.36% in 2005). In 2010, with a big UNS expected, I’d expect a slightly bigger than average standard deviation, so I'm setting 3% for this standard deviation.

For Con-Lib swings: standard deviations again about 3% (but very fractionally higher than Lab-Con swings, on average). Average standard deviation of 3.14%, maximum 3.34% (1987), minimum 2.97% (1997).

For Lab-Lib swings: standard deviation between 3.5% and 4%. Average of 3.77%, maximum 3.95% (1992), minimum 3.60% (2001).

So, in terms of odds. Work out how much swing is needed for the seat to fall. Compare to UNS. Leaving out the constituency size issue (which blurs it by a quarter to a half a percent either way, usually favourably to Labour), a seat where the swing required is exactly equal to the UNS would be – all things being equal – an even money shot. Exactly 50:50. That’s your baseline – you then judge from whatever factors you like whether that seat is more or less likely to fall. Region? Local strength? Which party will have superior targeting? Tactical voting and voting unwind? That kind of stuff. But you’d start from evens and adjust from there.

So I've put together a table showing the baseline starting odds in the Con/Lab battles.

Baseline Odds

Look at the swing required. Adjust for your best guess of targetting marginals and constituency sizes - add or subtract up to about 1.5% at most. Then cross reference below to get your starting odds, before you move them for local factors.

Or to put it another way – work out where the electoral tide has risen to and have that as the new “sea level”. The table below gives you the size of the waves (and troughs) – and how rare they are at that scale and you can use your judgement (based on local factors) as to the chances of them appearing at the constituency in question.

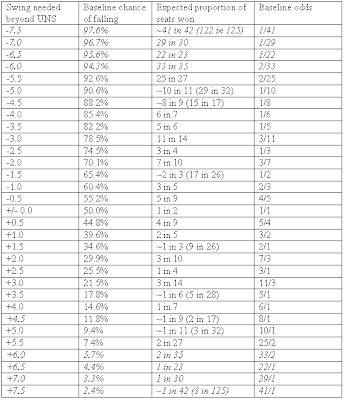
In the tables below, I’ve presented suggested “fair baseline odds” of the fluctuations being that large (if it were random). The percentage chance of falling is artificially precise – we don’t actually know yet what the standard deviations will be so I’ve estimated them – and I’ve made the translation into odds as “transparent” as possible so that you can make them more or less precise as you see fit. (Click on tables for larger image)

Conservative-Labour swing and Conservative-LibDem swing (estimated standard deviations of 3.0%)

*Treat the extremes with great caution – if the standard deviation is a bit off, it doesn’t take much to turn that 43/1 shot at 6.0% overshoot required into 11/1 (for 3.44% standard deviation) or 90/1 (for 2.36% standard deviation). The italicised area of the table is the area that most has to be used “with caution”- especially for Lab-Con swings (the LD-Con swings tend to have more regular fluctuations)

So for a seat which (adjusted) UNS says should be reduced to a 6% Labour majority, then your baseline odds on it falling should be 5/1 before using your judgement on local factors. For a seat where the Tory should be swept in with a 6% majority (needs to undershoot the swing by more than 3% not to be taken), the baseline odds should be 5/1 against the Labour incumbent holding.

Labour-LibDem swing (estimated standard deviation of 3.8%)

So there you have it. Use with care, as with all mathematical tools - but hopefully this will give a good starting point for each constituency analysis. The kind of thing I'm aiming for is: "XX should be 10/1 - poor local party performance, MP tainted by expenses, that region looking better for the Tories ... say 5/1. While YY should be 1/2 on, but strong local party performance, good local MP, demographics bad for the Tories ... call it evens".

Good luck.

Andy Cooke

(EDIT - Tables were initially wrong way round - now corrected)